電場與電力的基礎
電流流過物質時,必定存在有電場。電場到底是什麼呢?我們將從電場的基礎知識開始詳細解說,並介紹利用高斯定律計算電場的方法。
何謂電場
所謂電荷是指帶電物體所帶有的電量。相較於質子,如果電子較多為-,如果電子較少則為+。符號以Q表示,單位以C(庫倫)表示。假設兩個電荷量為Q1、Q2,距離為r[m],作用於兩個電荷之間的力為F[N],庫倫定律以下列公式表示。
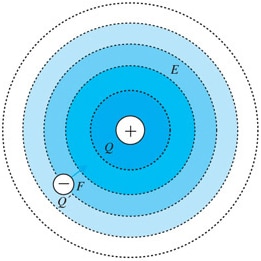
電場強度會從內側開始向外逐漸減弱。
電場是指存在於帶電物體周圍,且存在可對電荷產生作用之電力的區域。例如,某個空間中存在點電荷*,將會使周圍空間具有特殊性質,如果將另一個點電荷帶入該處,將會因為該空間的作用而使力作用於帶入到點電荷,亦即可將其視為「電荷的勢力範圍」。並且,如圖所示,其勢力會從中心逐漸向遠處而隨之減小。此電場的強度稱為「電場強度」,如圖所示,電場強度會從中心向外側展開,而且越遠就越弱。
由於此性質具有方向性,因此使用向量來表示。表示電場時,不僅與其強度有關,同時也與其方向有關。
*點電荷:在無法量測大小的極小物體上帶電的電荷
假設空間內存在點電荷Q[C],作用於該電荷上的力為F[N],此時電場強度為
E=F/Q[V/m]
電場的單位[V / m]表示每單位距離的電位差。反之則為
F=QE[N]
這是作用於電場中的電荷的力,亦即「庫倫力」。
根據以上公式,點電荷產生的電場強度為
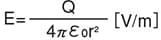
當存在具有電荷量Q[C]的點電荷時,其周圍空間的電場強度與點電荷的距離r[m]的平方成反比。
電力線
電場的方向是從正電荷朝向負電荷的方向。
所謂電力線是描繪電場方向的虛擬線,如下圖所示。電力線的方向表示電場,從正側朝向負側。
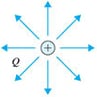
點電荷的電力線
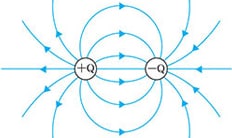
存在的電力線
如下圖所示,在帶電體(導體)的情況下,電力線從表面垂直而出。此時,如果帶電體的表面電荷帶有相同密度的電,則電力線也將處於相同間隔。密度表示電位的高度,我們可以看出,電力線較多且間隔較窄的部位,其電場較強,反之在電力線較少且間隔較寬的部位,其電場較弱。
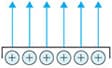
電力線
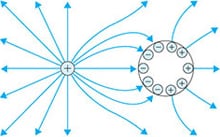
電力線
高斯定律
當電場中存在電荷時,有一種方法可根據電荷的量和形狀來計算電場。此方法稱為「高斯定律」,透過計算接近的帶電體作用於電場的電力,有助於防止靜電危害。
下表是「高斯定律」的計算公式。
下表的「高斯定律」顯示,計算相對於電荷分佈狀態的點或線周圍的電場時,帶電體的電容率與電場強度成反比,電力線的密度與電場強度成正比。換言之,如果是尖頭形狀,則該處的電力密度將變大,電場也將會提高。
| 電荷的形態 | 電荷量 | 電場[V/m] | ||
|---|---|---|---|---|
| 點電荷 | Q[C] | E=Q/4πε0r2 | ||
| 線電荷 | λ[C/m] | E=λ/2πε0r | ||
| 面電荷 | δ[C/m2] | 電場[V/m] | E=σ/ε0 | 導體 |
| E=σ/2ε0 | 絕緣體 | |||
| 圓柱 | ρ[C/m2] | 電場[V/m] | E=ρr/2ε0 | 圓柱內 |
| E=a2/2rε0 | 圓柱外 | |||
| 球 | ρ[C/m2] | 電場[V/m] | E=ρr/3ε0 | 球內 |
| E=ρa3/3ε0r2 | 球外 | |||
與帶電體中心的距離:r、帶電體半徑:a、真空介電常數:ε0
【例】
產生1[C]的點電荷的電場
點電荷與電場的距離為1[m]時,
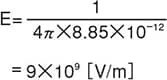
這相較於空氣中的絕緣擊穿強度3×106[V/m]約高出1000倍,相當於閃電的放電,因此並不實用。
例如,用布摩擦塑膠表面時的帶電量為每單位面積約為10-5[C/m2],因此表面帶電的電場如下。